Free fall and his effects on water splash

Objective:

To prove the difference of loss of water when throwing a ball in free fall from diferent heights and measuring how much water went out of the beaker.

Background information:

Free fall is what we call when an object is falling because of the force of gravity (9, 8 m/s² each second). When an object is in state of free fall, this one will accelerate according to gravity acceleration number wich has been said before. If we want to calculate the final velocity or any other reult affected by gravity, we use to use these equations called the kinematic equations: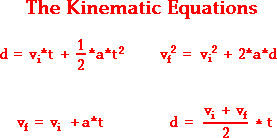

v­_i = Inicial velocity           v_f = final velocity

t = Time (in seconds)      a = acceleration (9, 8 m/s²)

d = distance

Images and information took from 

Physicsclassroom.com

Kinematic Equations

In-text: (Physicsclassroom.com, 2014)

Bibliography: Physicsclassroom.com, (2014). Kinematic Equations. [online] Available at: http://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations [Accessed 26 May. 2014].

Hypothesis:

The hypothesis is that when higher is the ball, more water will come out of the beaker because of the force of the impact.

Variables:
Independent: Height from where we throw the ball
Dependent: Loss of water in the beaker
Controlled: Mass of the plasticine ball

Materials:

- Waterproof scale

- Beaker of 10/15 cm of diameter

 - Plasticine ball

- Ruler

- Water

Procedure:

1. Fill the beaker with water.

2. Measure the weight of the water in the beaker

3. Throw the plasticine ball from 30 cm and meaure the lss of water (and so weight) done by the splash.

4. Repeat this process 2 times.

5. Do the same than in point 3. and 4. but at 50 cm

6. Then with 70 cm, 90 cm and 110 cm.

7. Put the results in a table and make the average between the three throw at the same height.

	Attempt 1 (mL)	Attempt 2 (mL)	Attempt 3 (mL)	Average
30 cm	4.2	4.6	4.2	4.3
50 cm	8.2	9.8	7.8	8.7
70 cm	14.8	13.2	15.0	14.3
90 cm	21.8	21.2	23.8	22.3
110 cm	19.8	22.4	20.6	21.4

Conclusion:

1.      We can observe that the more potencial energy we have the higher the water lost is. This is due to the fact that this potential energy it´s transformed into kinetic energy which is passes to the water which makes it move and some of it  goes out.

2.      Another thing we can see is that it is directly proportional. From our data  we can guess it forms a curve but we know that it´s not going to go to infinity since there´s a finite amount of water. Therefore it must be a hyperbola which tends to 1.3340 L (Our amount of water) when x goes to infinity and to 0 when it goes to –infinity

3.      We have to take into account our equipment is not perfect and maybe that´s why for example in 110cm we had some strange results compared with the ones we got on 90cm which is strange but it may have been cause the difference between this two is small and one has gone a bit up and the other a bit down.

b    We couldn´t be exact in the height despite having a device to measure so it can change +- 5 cm

2.      We couldn´t be sure if we threw it exactly in the centre of the bowl and this can have a big repercussion in the amount of water that goes out.